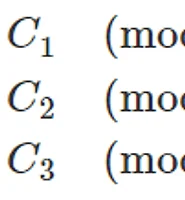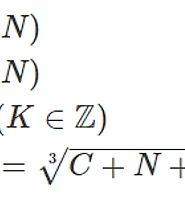Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- cryptography
- dns
- shellcode
- weak key
- Montgomery Reduction
- OverTheWire Bandit Level 1 → Level 2
- XSS
- rao
- arp
- dreamhack
- Crypto
- redirect
- spoofing
- Cube Root Attack
- overthewire
- RSA
- 웹해킹
- Franklin-Reiter Related Message Attack
- bandit
- picoCTF
- Bandit Level 1 → Level 2
- 시스템해킹
- 암호학
- 드림핵
- pycrpytodome
- AES
- return address overflow
- RSA Common Modulas Attack
- CSRF
- Hastad
Archives
- Today
- Total
암호(수학) 등.. 공부한 거 잊을거 같아서 만든 블로그
[Cryptography] Franklin-Reiter Related Message Attack 본문
Franklin-Reiter Related Message Attack
Franklin-Reiter Related Message Attack 은 두 개의 관련된 메세지에 대하여 동일한 RSA 키로 암호화 된 값을 알 때, 관련된 메세지의 값을 알 수 있는 공격이다.
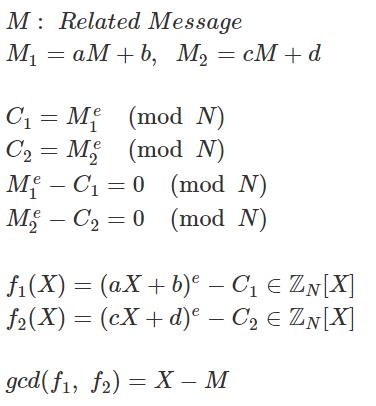
M이라는 메세지와 관련된 메세지인 M1, M2 메세지의 암호화 값인 C1, C2를 알고 있으면 M값을 구할 수 있다.
두 방정식 f1, f2는 X = M 일 경우 0을 값으로 가진다. ( f1(M) = f2(M) = 0 )
즉, X-M 을 공통 인수로 가지게 되어 gcd 알고리즘을 통해 f1, f2의 공통 인수 X-M을 구할 수 있으며,
구해진 인수 X-M의 상수항 -M에 N을 더함으로 M을 구하게 된다.
RSA의 공개키 e가 3일 경우 공통 인수는 일차식으로 나오게 되지만 e가 3이 아닐 경우 일차식이 아닌 경우가 있다.
일차식이 아닌 경우 공격에는 실패하게 된다.
아래의 코드는 Franklin-Reiter Related Message Attack 의 예시를 파이썬 언어로 나타낸 코드이다.
poc.py
# poc.sage
from sage.all import *
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
M = b"cryptography"
M1 = M + b" is hard"
M2 = b"I hate " + M
e = 3
p, q = getPrime(512), getPrime(512)
N = p * q
c1 = pow(bytes_to_long(M1), e, N)
c2 = pow(bytes_to_long(M2), e, N)
def gcd(a, b):
while b:
a, b = b, a % b
return a.monic()
a = 2 ** (8 * len(b" is hard"))
b = bytes_to_long(b" is hard")
c = 1
d = bytes_to_long(b"I hate ") * (2 ** (8 * len(M)))
# preparse("P.<X> = PolynomialRing(Zmod(N))")
P = PolynomialRing(Zmod(N), names=("X",))
(X,) = P._first_ngens(1)
g1 = (a * X + b) ** e - c1
g2 = (c * X + d) ** e - c2
result = -gcd(g1, g2)
print(f"M = {long_to_bytes(int(result[0])).decode()}")
실행 결과
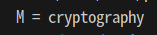
M1, M2 의 공통된 부분인 M을 복호화 해낸 것을 볼 수 있다.
'Cryptography' 카테고리의 다른 글
| [Cryptography] 암호 공부 관련 웹 사이트, 도서 링크 (0) | 2024.04.18 |
|---|---|
| [Cryptography] Weak Key (0) | 2024.03.16 |
| [Cryptography] Hastad's Broadcast Attack (0) | 2024.02.13 |
| [Cryptography] RSA Cube Root Attack (0) | 2024.02.03 |
| [Cryptography] RSA Common Modulas Attack (0) | 2024.01.27 |