Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- Bandit Level 1 → Level 2
- 시스템해킹
- overthewire
- weak key
- Hastad
- dreamhack
- XSS
- Franklin-Reiter Related Message Attack
- 암호학
- AES
- 드림핵
- shellcode
- OverTheWire Bandit Level 1 → Level 2
- 웹해킹
- CSRF
- Cube Root Attack
- Montgomery Reduction
- RSA
- redirect
- RSA Common Modulas Attack
- cryptography
- arp
- spoofing
- bandit
- rao
- pycrpytodome
- dns
- Crypto
- picoCTF
- return address overflow
Archives
- Today
- Total
목록Montgomery Reduction (1)
암호(수학) 등.. 공부한 거 잊을거 같아서 만든 블로그
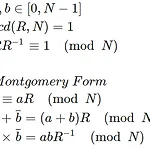 [Algorithm] Montgomery Reduction Algorithm
[Algorithm] Montgomery Reduction Algorithm
Montgomery Form 위 이미지에 있는 계산 방식은 Montgomery From 이라고 하는 계산방법이다. 몽고메리 폼에서의 a` = aR mod N와 b` = bR mod N을 곱하면 (aR mod N) * (bR mod N) = (abR)R mod N 이고, 이를 몽고메리 폼에 맞게 하기 위해 R^(-1)을 곱해준다. (abR)R*R^(-1) mod N =(abR) mod N 이러한 계산과정은 R^(-1)을 곱하고 N을 나눠야 하기 때문에 느리다. 하지만 아래의 알고리즘을 통하여 구하면 비트 쉬프트 연산을 통해 빠른 계산으로 구할 수 있다. Montgomery Reduction Algorithm아래의 수식은 몽고메리 감산 알고리즘으로 T = (aR mod N) * (bR mod N)을 (abR..
Algorithm
2024. 3. 27. 16:38
