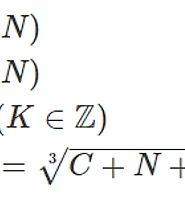| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- arp
- overthewire
- dreamhack
- rao
- RSA
- CSRF
- OverTheWire Bandit Level 1 → Level 2
- shellcode
- dns
- Crypto
- Franklin-Reiter Related Message Attack
- picoCTF
- cryptography
- Hastad
- RSA Common Modulas Attack
- 암호학
- 시스템해킹
- XSS
- AES
- return address overflow
- spoofing
- 드림핵
- Montgomery Reduction
- redirect
- weak key
- Bandit Level 1 → Level 2
- bandit
- 웹해킹
- Cube Root Attack
- pycrpytodome
- Today
- Total
암호(수학) 등.. 공부한 거 잊을거 같아서 만든 블로그
[Cryptograhpy] AES (Advanced Encrytion Standard) 본문
AES (Advanced Encrytion Standard)
AES 암호는 블록암호로 SPN (Substitution Permutation Network) 구조를 가지며, 블록의 크기는 총 128 bit (16 byte) 이고, key의 길이는 128, 192, 256 이 있다.
블록은 평문을 128 bit 씩 나눈 값들을 말하며, 암호화 할 때 블록들을 내부 상태 (state) 라 부르는 각각의 성분이 1 byte 인 4 by 4 행렬로 다루게 된다.

평문 블록의 바이트값이 s0, s1, ~ , s15 순서로 내부 상태에 배치된다.
key의 길이에 따라 10, 12, 14개의 라운드를 가지고 있으며 키 스케쥴 함수 (KeyExpansion) 과 4가지의 연산 (AddRoundKey, SubBytes, ShiftRows, MixColumns) 을 통하여 암복호화를 수행한다.
키 스케쥴을 통해 확장된 키는 AddRoundKey 연산에서 사용된다.
AES 키 길이에 따른 라운드 수
| Key Length (bit) | Round | |
| AES-128 | 128 | 10 |
| AES-192 | 192 | 12 |
| AES-256 | 256 | 14 |

AES 암호화
AES의 암호화 과정은 다음 이미지와 같다.

위 이미지에서 r은 라운드 수로 key의 길이가 128이면 r = 10, 192 이면 r = 12, 256 이면 r = 14 로 r 의 값이 결정된다.
AES 는 KeyExpantion 을 통하여 총 라운드 수 만큼의 128bit 값들을 (K1, K2, ... , Kr) 생성하고, 이를 AddRoundKey 연산에서 사용한다.
암호화 과정은 상태에 AddRoundKey 를 한 후, 라운드를 (총 라운드 수 - 1) 만큼 반복하고 마지막으로 SubBytes, ShiftRows, AddRoundkey 연산을 해서 암호문을 생성한다.
AES 복호화
복호화 과정은 암호화 과정의 역순으로 진행되며, 사용된 함수들 또한 역함수를 사용한다.

AddRoundKey 는 라운드 키와 단순히 xor 연산만 하므로 역변환이 동일하지만, ShiftRows, SubBytes, MixColumns 는 역변환이 다르다. 역변환 함수를 InvShiftRows, InvSubBytes, InvMixColumns 라 하겠다.
AES 구성 알고리즘
AddRoundKey

AddRoundKey는 상태와 해당하는 라운드의 키를 xor 연산을 한 것이다.
상태의 성분 각각의 값은 S_i ^ K_i 의 값을 가지게 된다.
역변환은 라운드 키를 상태에 xor 연산을 하는 것으로 AddRoundKey와 같은 변환임을 알 수 있다.
SubBytes
SubBytes는 S-box라는 테이블의 값으로 치환 연산을 한다.

예를 들어 16 이라는 바이트가 있을 때, 이를 10 과 06 으로 쪼개서 해당하는 값인 47로 치환한다.
InvSubBytes
SubBytes 의 역변환인 InvSubBytes는 S-box의 역참조 테이블인 Inverse S-box 를 이용하여 값을 치환한다.
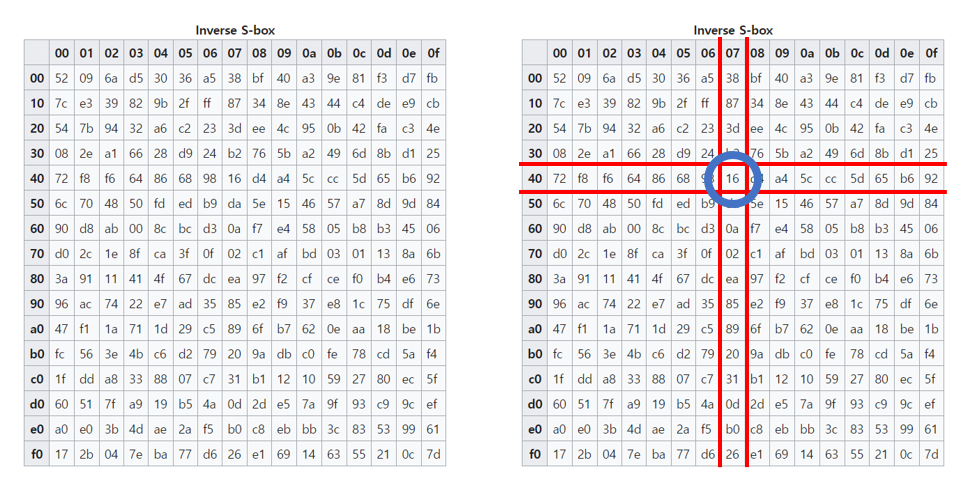
실제로 SubBytes에서 예시를 들었던 16에 대해서 16 의 변환 값이 47 이므로
Inverse S-box 의 40 행 07 열 을 보면 16 이 있는 것을 확인할 수 있다.
ShiftRows
ShiftRows 는 상태 i 번째 행에 i - 1 번 만큼 왼쪽으로 순환이동 하는 연산으로 1행의 경우 0번 순환이동하고, 2행의 경우 왼쪽으로 1번 만큼 순환이동한다.
예를 들어 (a, b, c, d) 를 왼쪽으로 1번 순환이동하면 (b, c, d, a) 가 된다.

- 1행 : ShiftRows(S0, S4, S8, S12) => (S0, S4, S8, S12), 1 - 1 = 0 만큼 왼쪽으로 순환이동
- 2행 : ShiftRows(S1, S5, S9, S13) => (S5, S9, S13, S1), 2 - 1 = 1 만큼 왼쪽으로 순환이동
- 3행 : ShiftRows(S2, S6, S10, S14) => (S10, S14, S2, S6), 3 - 1 = 2 만큼 왼쪽으로 순환이동
- 4행 : ShiftRows(S3, S7, S11, S15) => (S15, S3, S7, S11), 4 - 1 = 3 만큼 왼쪽으로 순환이동
InvShiftRows
ShiftRows 의 역변환인 InvShiftRows 는 ShiftRows의 순환이동 방향을 오른쪽으로만 바꿔주면 된다.

아래 이미지를 통해 ShiftRows 의 역변환이 InvShiftRows 임을 확인할 수 있다.

MixColumns
MixColumns는 특정한 행열을 상태에 행렬곱 하는 연산이다.
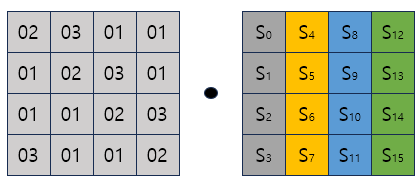
이떄 행렬곱에서의 연산은 실생활에서 쓰는 덧셈이나 곱셈과는 다른
갈루아 필드 GF(2^8) 라는 대수적 구조 에서의 연산을 한다. 자세하게는 다루지는 않고 연산하는 방법에 대해서만 다루겠다.
덧셈 연산
계산을 할 때에는 한 바이트씩을 다항식으로 변환하여 계산한다,
예를 들어 10001011 라는 이진수를 다항식으로 x^7 + x^3 + x^1 + 1 로 변환 된다.
표현한다.
x^7 + x^3 + x^1 + 1 (10001011) 를 x^7 + x^5 + x^3 + 1 (10101001) 에 더해보겠다.
(x^7 + x^3 + x^1 + 1) + (x^7 + x^5 + x^3 + 1) = 2x^7 + x^5 + 2x^3 + x^1 + 2
2x^7 + x^5 + 2x^3 + x^1 + 2 가 나왔는데 이 식의 모든 계수에 2를 나눈 나머지를 그대로 계수에 적용 한다.
-1 % 2 = 1, 1 % 2 = 1, 2 % 2 = 0, -2 % 2 = 0, 0 % 2 = 0
이 사실을 2x^7 + x^5 + 2x^3 + x^1 + 2 에 적용하면,
2x^7 + x^5 + 2x^3 + x^1 + 2 = x^5 + x^1 (00100010) 이 된다.
또한 이 결과가 xor 연산임을 알 수 있다. 10001011 xor 10101001 = 00100010
따라서 덧셈 연산은 xor 연산을 한다.
곱셈 연산
곱셈은 바이트들의 다항식표현을 더이상 인수분해가 되지 않는 기약 다항식인 x^8 + x^4 + x^3 + x^1 + 1 으로 나누어서 나온 나머지가 곱셈의 결과가 된다.
여기서 주의 해야할 점은
덧셈에서 했던것처럼 연산의 결과에는 항상 다항식의 모든 계수에 2를 나눈 나머지를 그대로 계수에 적용 하는 변환을 해주어야 한다.
예시는 덧셈을 예를 들 때, 사용했던 다항식으로 예를 들겠다.
먼저 x^7 + x^3 + x^1 + 1 (10001011) 와 x^7 + x^5 + x^3 + 1 (10101001) 를 곱하면 다음과 같다.
(x^7 + x^3 + x^1 + 1) * (x^7 + x^5 + x^3 + 1) =
x^14 + x^12 + 2x^10 + x^9 + 2x^8 + 2x^7 + 2x^6 + x^5 + 2x^3 + x + 1
여기서 각 계수들을 2로 나누어 주면 x^14 + x^12 + x^9 + x^5 + x + 1 가 되는데 이를 x^8 + x^4 + x^3 + x^1 + 1 로 나눈 결과는 다음과 같다.
몫 : x^6 + x^4 + x^2 + 1 나머지 : x^5 + x^2 (00100100)
여기서 나머지가 곱셈의 결과이다.
x^7 계수가 1 일때의 다항식 (최상위 비트가 1)
x^7 + ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g 에 x (2 = 00000010) 를 곱셈 연산을 해보자.
(a, b, c, d, e, f, g 는 0 이거나 1)
(x^7 + ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g) * x = (x^8 + ax^7 + bx ^6 + cx^5 + dx^4 + ex^3 + fx^2 + gx)
x^8 + ax^7 + bx ^6 + cx^5 + dx^4 + ex^3 + fx^2 + gx 를 x^8 + x^4 + x^3 + x^1 + 1 로 나눈 나머지를 구하면
ax^7 + bx ^6 + cx^5 + (d-1)x^4 + (e-1)x^3 + fx^2 + (g-1)x + 1 이다.
연산하기 전의 다항식인 x^7 + ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g 를 P 라 할 때,
P 에 x를 곱셈 연산 한 후의 결과인 ax^7 + bx ^6 + cx^5 + (d-1)x^4 + (e-1)x^3 + fx^2 + (g-1)x + 1 와 비교해보면
P 를 왼쪽으로 한번 쉬프트 연산을 한 후에 0x1b와 xor 한 결과와 동일하다.
P = (x^7 + ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g) << 1 = (ax^7 + bx ^6 + cx^5 + dx^4 + ex^3 + fx^2 + gx)
(ax^7 + bx ^6 + cx^5 + dx^4 + ex^3 + fx^2 + gx) xor (x^4 + x^3 + x + 1) (00011011 0x1b)
= ax^7 + bx ^6 + cx^5 + (d-1)x^4 + (e-1)x^3 + fx^2 + (g-1)x + 1
이번에는
x^7 계수가 0 일때의 다항식 (최상위 비트가 0)
ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g 에 x (2 = 00000010)를 곱셈 연산을 해보자.
(ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g) * x = x^7 + ax^7 + bx ^6 + cx^5 + dx^4 + ex^3 + fx^2 + gx
이므로 왼쪽으로 쉬프트 이동을 한번 한 결과와 동일하다.
(ax^6 + bx ^5 + cx^4 + dx^3 + ex^2 + fx^1 + g) << 1 = x^7 + ax^7 + bx ^6 + cx^5 + dx^4 + ex^3 + fx^2 + gx
정리하자면
임의의 1 바이트인 a 에 대하여 2를 곱하는 연산은 다음과 같다.
a의 최상위 비트가 1 인 경우 : a * 2 = (a << 1) xor 0x1b
a의 최상위 비트가 0인 경우 : a * 2 = (a << 1)
로 계산한다.
위 사실을 이용하여 고속 거듭제곱 알고리즘으로 구현하면 된다. (맨 하단 구현 참고)
InvMixColumns
MixColumns 의 역변환인 InvMixColumns 의 경우 MixColumns 에 사용되었던 행렬의 역행열에 상태를 행렬곱 한다.
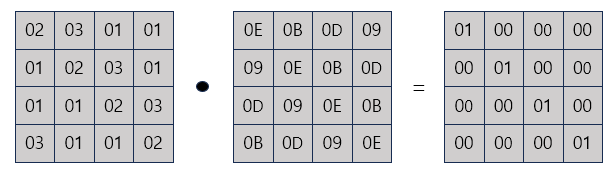

암호화 과정에서 상태에 곱해진 행렬을 복호화 과정에서 행렬의 역행렬을 곱하므로 곱해진 행렬의 값을 제거해서 원래의 상태 값을 구할 수 있다.

KeyExpansion
keyExpansion 은 AddRoundKey 연산에 필요한 라운드 키를 라운드의 횟수에 맞게 키를 확장한다.
조금더 자세하게 말하자면 원래의 키 값에서 연산을 통해 열을 확장시킨다.
라운드가 r 일 경우 암호화 과정에서 처음에 AddRoundKey 를 할 값 1 개, 라운드 키 r 개 총 r + 1 개의 128 bit 값이 필요하다.
따라서 keyExpansion 통해 키 의 값을 r * 128 bit 만큼 확장하여 기존의 키값과 합쳐 총 (r + 1) * 128 bit 만큼의 값을 만들어서 128bit 단위로 나누어 AddRoundKey 연산에 사용한다.
keyExpantion 에서는 RotWord 와 SubBytes, xor 연산을 사용해서 키를 확장한다.
RowWord 는 아래 이미지 처럼 (K12, K13, K14, K15) 를 위로 1번 순환이동 하는 연산이다.

SubByte는 위에서 살펴본대로 s-box의 해당하는 값들로 치환하는 연산이다.
또한 키를 확장할 때, Round Constant 라는 값들을 xor 연산에 사용한다.

AES-128
이제 AES-128에서의 KeyExpantion 을 살펴보자.

키를 4x4 행렬로 나타낼때, 각각의 열을 0, 1, 2, 3 열이라 하겠다. (열을 0부터 새겠다)
keyExpantion 을 통해 키를 확장할 때, 4의 배수가 되는 열을 생성할때는 위 이미지의 연산을 적용해야한다.
위 이미지의 상황은 키를 확장하여 4열을 생성하려고 한다.
4 는 4 의 배수 이기 때문에 위 이미지에서 적용하는 연산을 통하여 4열을 생성한다.
이를 일반화 하면
4의 배수인 열을 i 라 하면
i - 1 열에 RotWord를 적용시키고, SubBytes 를 한 후, i - 4 열과 xor 하고 rc의 i / 4 - 1 열 값과 xor 한다.
즉 n열의 값을 W(n), rc 의 n열 값을 rc(n) 이라 할 때,
W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - 4) xor rc(i / 4 - 1) 이다.
여기서 i / 4 는 i 를 4로 나눈 몫의 값을 의미한다.

생성하려는 열이 4의 배수가 아니면 위 이미지의 연산을 적용하여 열을 생성한다.
4의 배수가 아닌 열을 i 라 하면,
W(i) = W(i - 1) xor W(i - 4)
아래 이미지를 통해 8열과 그 외의 열에도 앞서 했던것처럼 동일한 연산이 적용되는 것을 볼 수 있다.


연산을 정리하자면,
i = 0, 1, 2, 3 : W(i) = W(i)
i 가 4의 배수일 때 : W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - 4) xor rc(i / 4 - 1)
i 가 4의 배수가 아닐 때 : W(i) = W(i - 1) xor W(i - 4)
이고, 이를 i = 4 * (10 + 1) - 1 = 43 까지 반복한다.
AES-128 은 라운드가 10 개이므로 총 128 bit 키 11개가 필요하다.
따라서 128 bit 을 4x4 행렬로 타나내면 열이 총 4개이므로 11 * 4 = 44 개의 열이 필요하고,
0 ~ 43 까지 총 44개의 열이므로 i = 4 * (10 + 1) - 1 까지 반복하는 것이다.
W(0), W(1), ... , W(43)
AES-192
AES-192 에서의 KeyExpantion은 AES-128과 한가지 차이점을 제외하고는 동일하다.
그 차이점은 키를 행렬로 표현했을 때의 행값이 6이라는 것이다.
AES-128에서는 키가 128 bit 이기 때문에 이를 4x4 행렬로 나타내어 계산했다.
AES-192 는 키가 192 bit 이기 때문에 4x6 행렬로 표현되며 따라서,
AES-128에 했던 연산이 행이 4일때에 한 연산을 AES-192 에서는 행이 6일 때 하면 된다.
AES-128 의 KeyExpantion 과정이 다음과 같다고 했는데
i = 0, 1, 2, 3 : W(i) = W(i)
i 가 4의 배수일 때 : W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - 4) xor rc(i / 4 - 1)
i 가 4의 배수가 아닐 때 : W(i) = W(i - 1) xor W(i - 4)
이를 AES-192 에 맞게 변환하여 식의 4를 6으로 바꿔주기만 하면 된다.
따라서 AES-192의 KeyExpantion 은 다음과 같다.
i = 0, 1, 2, 3, 4, 5 : W(i) = W(i)
i 가 6의 배수일 때 : W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - 6) xor rc(i / 6 - 1)
i 가 6의 배수가 아닐 때 : W(i) = W(i - 1) xor W(i - 6)
그리고, 이를 i = 4 * (12 + 1) - 1 = 51 까지 반복한다.
W(0), W(1), ... , W(51)


AES-256
앞에서 AES-128 과 AES-192의 KeyExpantion 을 보고 AES-256을 유추해 볼 수 있다.
AES-256의 키가 256 bit 이므로 4x8 행렬로 표현이 가능하며 따라서 다음과 같은 식이 나온다.
i = 0, 1, 2, 3, 4, 5, 6, 7 : W(i) = W(i)
i 가 8의 배수일 때 : W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - 8) xor rc(i / 8 - 1)
i 가 8의 배수가 아닐 때 : W(i) = W(i - 1) xor W(i - 8)
하지만 AES-256 에서는 한가지가 더 추가된다.
i % 8 = 4 일 경우 : W(i - 8) xor SubBytes(W(i - 1))
i % 8 은 i 를 8 로 나누었을 때의 나머지를 나타낸다.
정리하면 AES-256에서의 KeyExpantion은 다음과 같다.
i = 0, 1, 2, 3, 4, 5, 6, 7 : W(i) = W(i)
i 가 6의 배수일 때 : W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - 8) xor rc(i / 8 - 1)
i 가 6의 배수가 아닐 때 : W(i) = W(i - 1) xor W(i - 8)
i % 8 = 4 일 경우 : W(i - 8) xor SubBytes(W(i - 1))
그리고, 이를 i = 4 * (14 + 1) - 1 = 59 까지 반복한다.
AES-128, AES-192, AES-256의 KeyExpantion 연산을 살펴 보았다.
128, 192, 256의 KeyExpantion 을 하나로 정리해서 표현하자면 다음과 같다.
N_k = (Key Length) / 32
N_b = (Block Length) / 32 = 128 / 32 = 4
N_r = 총 라운드 수
W(i) : W의 i 행
rc(i) : Round Constant 의 i 행
아래의 식을 i = 0 부터 i = N_b(N_r + 1) - 1 까지 반복
i = 0, 1, 2, ... (N_k - 1), : W(i) = W(i)
i 가 N_k의 배수이면 : W(i) = SubBytes( RotWord( W(i - 1) ) ) xor W(i - N_k) xor rc(i / N_k - 1)
N_k > 6 이고 i % N_k = 4 이면 : W(i) = W(i - N_k) xor SubBytes(W(i - 1))
i 가 N_k의 배수가 아니면 : W(i) = W(i - 1) xor W(i - N_k)
구현
아래 깃허브 주소에 Python, C++로 AES구현한 코드가 있으니 필요하면 참고하길 바란다.
https://github.com/heahgo/PyCrypto/tree/main/PyCrypto/Cipher/AES
https://github.com/heahgo/CppCrypto/tree/main/crypto/aes
참고 자료
http://www.formaestudio.com/rijndaelinspector/
https://en.wikipedia.org/wiki/Finite_field_arithmetic
https://en.wikipedia.org/wiki/Rijndael_S-box
Joan Daemen, Vincent Rijmen the design of rijndael: aes - the advanced encryption standard
'Cryptography' 카테고리의 다른 글
| [Cryptography] Hastad's Broadcast Attack (0) | 2024.02.13 |
|---|---|
| [Cryptography] RSA Cube Root Attack (0) | 2024.02.03 |
| [Cryptography] RSA Common Modulas Attack (0) | 2024.01.27 |
| [Cryptograhpy] AES-ECB (Electronic Code Book) 운영 모드 (0) | 2023.07.07 |
| [Cryptograhpy] CRT를 이용한 빠른 RSA 복호화 (0) | 2022.10.29 |