| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- weak key
- RSA Common Modulas Attack
- spoofing
- return address overflow
- pycrpytodome
- XSS
- Bandit Level 1 → Level 2
- RSA
- Franklin-Reiter Related Message Attack
- 웹해킹
- 시스템해킹
- redirect
- AES
- picoCTF
- rao
- overthewire
- Hastad
- Montgomery Reduction
- 암호학
- CSRF
- Cube Root Attack
- arp
- dreamhack
- OverTheWire Bandit Level 1 → Level 2
- cryptography
- 드림핵
- dns
- shellcode
- Crypto
- bandit
- Today
- Total
암호(수학) 등.. 공부한 거 잊을거 같아서 만든 블로그
확장 유클리드 알고리즘 (Extended Euclidean Algorithm) 본문
유클리드 알고리즘
유클리드 알고리즘이란?
유클리드 알고리즘이란 두 정수의 최대 공약수를 효율적으로 구하는 방법으로써 다음 정리를 이용한다,
a = bp + r (0 <= r < b) 일 때, gcd(a, b) = gcd(b, r)
gcd(a, b) 는 a 와 b의 최대공약수를 의미한다.
gcd(a, b) = gcd(b, r) 이 성립함을 증명

예시
28과 24의 최대 공배수를 구해보면
28 = 24 * 1 + 4
gcd(28, 24) = gcd(24, 4)
24 = 4 * 6 + 0
gcd(24, 4) = 4
즉, gcd(28, 24) = gcd(24, 4) = 4
이므로 28과 4의 최대 공배수가 4 임을 알 수 있다.
구현 (파이썬)

gcd(a, b) = gcd(b, r) 이라는 것을 이용하여 계속반복해보면 위와같은 점화식이 나오는 것을 알 수 있다.
그리고 위의 점화식이 유클리드 알고리즘 동작의 핵심이다.
유클리드 알고리즘의 과정을 말로 표현해보면
먼저 두 수를 a, b라는 변수에 저장을 한다.
1. b가 0이면 멈추고 a(최대공약수)를 반환한다.
2. a를 b로 나눈 나머지를 변수 r에 저장한다.
3. a에 b값을 저장하고, b에는 r값을 저장한다. 1단계로 돌아간다.
이를 파이썬으로 구현하면 다음과 같다.
euclidean_algorithm.py
# euclidean_algorithm.py
# Time Complexity : O(log(min(a, b)))
def gcd(a, b): # Greatest Common Divisor with Euclidean Algorithm
while b != 0:
r = a % b
a, b = b, r
return a
if __name__ == '__main__':
first_int, second_int = map(int, input("Input two integers (example 12 18) : ").split(' '))
print(f'gcd({first_int}, {second_int}) = {gcd(first_int, second_int)}')확장 유클리드 알고리즘
확장 유클리드 알고리즘이란
확장 유클리드 알고리즘은 기존 유클리드 알고리즘을 이용하여 a * s + b * t = gcd(a, b) 이 성립하는 두 임의의 정수 s 와 t를 구하는 알고리즘이다.
임의의 두 정수 s, t에 대해서, a * s + b * t = gcd(a, b) 가 성립한다. 이를 베주 항등식이라 한다. 증명은 아래 이미지를 참고하자.

원리

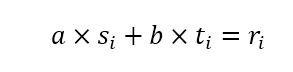
r0 = a, r1 = b 라 하면 s0 = 1, s1 = 0, t0 = 0, t1 = 1 임을 알 수 있으며 위와 같은 식으로 r을 표현할 수 있다.
오타)
위 사진위 수식 첫번째 줄에서 r0 = a1 이 아니라 r0 = a이다.
( r의 값을 차례대로 풀어보면 a*s + b*t 의 꼴로 r을 표현할 수 있음을 알 수 있다. )

우리는 유클리드 알고리즘을 알아가는 과정에서 위와 같은 점화식이 있다는 것을 알았다.
위 식의 r 값인 a * s + b * t를 점화식의 각각의 r에 대입해보면 다음과 같은 점화식을 얻게 된다.
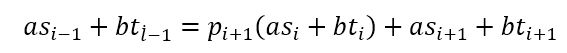


위의 두 점화식을 이용하여 s와 t 값을 구할 수 있다.
구현 (파이썬)
이를 파이썬으로 구현하면 다음과 같다.
extended_euclidean_algorithm.py
# extended_euclidean_algorithm.py
# Time Complexity : O(log(min(a, b)))
def extended_euclidean_algorithm(a,b): # a * s + b * t = gcd(a, b)
r0, r1 = a, b
s0, s1, t0, t1 = 1, 0, 0, 1
while(r1):
q = r0 // r1
temp = r0 - r1 * q
r0 = r1
r1 = temp
temp = s0 - s1 * q
s0 = s1
s1 = temp
temp = t0 - t1 * q
t0 = t1
t1 = temp # if gcd(a, b) == 1 then s0 is modular inverse (a mod b)
# r0 is gcd(a, b)
return (a, s0, b, t0, r0) # a * s0 + b * t0 = r0
if __name__ == '__main__':
first_int, second_int = map(int, input("Input two integers (example 12 18) : ").split(' '))
result = extended_euclidean_algorithm(first_int, second_int)
print(f'{result[0]} * {result[1]} + {result[2]} * {result[3]} = {result[4]}')
print(f'gcd({first_int}, {second_int}) = {result[4]}')
if result[4] == 1:
print(f'modular inverse (a mod b) : ', end = '')
print(result[1]) if result[1] > 0 else print(result[2] + result[1])
모듈러 역원 구하기
확장 유클리드 알고리즘을 통하여 모듈러 연산의 역원을 구할 수 있다.
먼저 역원이라 함은 gcd(a, n) = 1인, a와 n이 있을 때, a * a(^-1)≡ 1 mod n 을 만족하는 a^(-1)을 모듈 n에 대한 a 의 역원이라 한다.
a * a(^-1)≡ 1 mod n 은 n * p + a * a^(-1) = 1 꼴로 나타낼 수 있으며,
따라서 확장 유클리드 알고리즘을 이용하여 모듈 n에 대한 a의 역원인 a^(-1)을 구할수 있다.
예를 들어보면 13 mod 17의 역원을 구하려면 위에서 구현한 함수를 이용해서 extended_euclidean_algorithm(13, 17)의 return 받은 s0의 값이 역원이 되는 것을 알 수 있다.
참고
The Extended Euclidean Algorithm
In order to analyze Algorithms 2 and 3 we introduce the following matrices with coefficients in . Then, we define The following proposition collects some invariants of the Extended Euclidean Algorithm. Proof. We prove and by induction on . The case follow
www.csd.uwo.ca
'Algorithm' 카테고리의 다른 글
| [Algorithm] Montgomery Reduction Algorithm (0) | 2024.03.27 |
|---|---|
| 이진 탐색 알고리즘 (Binary Search Algorithm) (0) | 2023.05.10 |
| 모듈러 거듭제곱 연산 (modular exponentiation) (0) | 2022.07.25 |
| 버블 정렬 (Bubble Sort) (0) | 2022.07.18 |




