Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- pycrpytodome
- weak key
- 암호학
- spoofing
- CSRF
- dreamhack
- 시스템해킹
- Cube Root Attack
- RSA Common Modulas Attack
- OverTheWire Bandit Level 1 → Level 2
- overthewire
- RSA
- redirect
- XSS
- 드림핵
- Bandit Level 1 → Level 2
- picoCTF
- Crypto
- Montgomery Reduction
- arp
- dns
- Franklin-Reiter Related Message Attack
- rao
- shellcode
- Hastad
- bandit
- return address overflow
- 웹해킹
- AES
- cryptography
Archives
- Today
- Total
암호(수학) 등.. 공부한 거 잊을거 같아서 만든 블로그
모듈러 거듭제곱 연산 (modular exponentiation) 본문
개요
일반적으로 매우 큰 지수승의 수에 대해서 연산하는 것은 많은 자원을 이용해야한다. 특히 모듈러 연산 x**e (mod n) 대해서 e가 크면 클수록 매우 많은 공간과 시간을 써야한다. 하지만 모듈러 연산의 성질을 이용하여 연산의 속도를 매우 크게 향상 시킬 수 있다.
모듈러 연산의 성질
이 모듈러 연산에 대해서 여러가지 성질이 있지만 이 글에서 다룰 성질은 단 두가지이다.
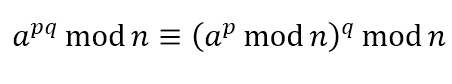
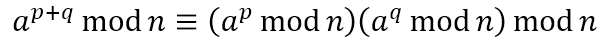
빠른 모듈러 거듭제곱 연산
과정과 원리
아래의 예시로 설명하겠다.
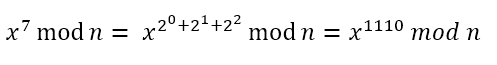
먼저 우리가 나눌 대상인 x의 지수 7를 2의 제곱의 합으로 나타낸다.
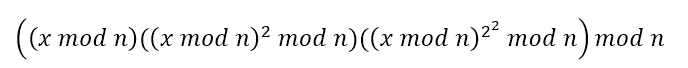
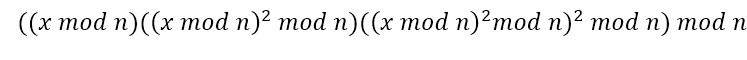
모듈러 연산의 성질을 이용하여 위와 같은 형태로 변환하고 계산한다.
기존 지수의 대한 연산은 밑을 그 지수의 계수만큼 곱하는 연산이 이루어진다. 하지만 모듈러연산에서는 지수에 대한 연산을 위와같이 변환하여 계산하므로 기존 지수의 제곱을 하는 것 보다 계산의 필요한 공간과 시간이 크게 줄어든다.
코드 구현 (파이썬)
# modular_exponentiation.py
# Time Complexity : O(logn)
def mod_exp_r2l(a, n, m): # right to left (r2l)
n = bin(n)[2:]
A, B = 1, a
for i in range(len(n) - 1, -1, -1):
if n[i] == '1':
A = pow(A*B, 1, m)
B = pow(B, 2, m)
return A
def mod_exp_l2r(a, n, m): # left to right (l2r)
if (n < 2):
return a ** n % m
n = bin(n)[3:] # Use less memory than r2l
A = a
for i in n:
A = pow(A, 2, m)
if i == '1':
A = pow(A * a, 1, m)
return A
if __name__ == "__main__":
first_int, second_int, third_int = map(int, input("Input a, n, m (example 17 9 31) : ").split(' '))
print('a ^ n mod m')
print(f'mod_exp_r2l : {mod_exp_r2l(first_int, second_int, third_int)}')
print(f'mod_exp_l2r : {mod_exp_l2r(first_int, second_int, third_int)}')
print(f'python pow : {pow(first_int, second_int, third_int)}' )
r2l 과 l2r 의 차이점은 l2r 이 r2l 보다 저장공간을 적게 쓴다는 점이다.
시간복잡도는 연산 대상의 지수를 이진수로 변환하여 이진수의 자릿수만큼 반복하게 된다.
따라서 O(logn)으로 시간복잡도를 나타낼 수 있다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] Montgomery Reduction Algorithm (0) | 2024.03.27 |
|---|---|
| 이진 탐색 알고리즘 (Binary Search Algorithm) (0) | 2023.05.10 |
| 버블 정렬 (Bubble Sort) (0) | 2022.07.18 |
| 확장 유클리드 알고리즘 (Extended Euclidean Algorithm) (0) | 2022.07.18 |




