[Algorithm] Montgomery Reduction Algorithm
Montgomery Form
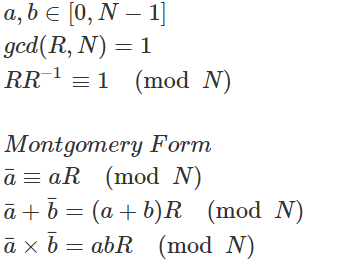
위 이미지에 있는 계산 방식은 Montgomery From 이라고 하는 계산방법이다.
몽고메리 폼에서의 a` = aR mod N와 b` = bR mod N을 곱하면
(aR mod N) * (bR mod N) = (abR)R mod N 이고, 이를 몽고메리 폼에 맞게 하기 위해 R^(-1)을 곱해준다.
(abR)R*R^(-1) mod N =(abR) mod N 이러한 계산과정은 R^(-1)을 곱하고 N을 나눠야 하기 때문에 느리다.
하지만 아래의 알고리즘을 통하여 구하면 비트 쉬프트 연산을 통해 빠른 계산으로 구할 수 있다.
Montgomery Reduction Algorithm
아래의 수식은 몽고메리 감산 알고리즘으로
T = (aR mod N) * (bR mod N)을 (abR) mod N 이 되게 하여 몽고메리 폼에 맞게 변환하는 알고리즘이다.

.
1번을 보면 T mod R 연산을 하는데 R이 2의 거듭제곱이면 T를 비트로 표현할 때, R 이상의 비트를 날리면 T mod R을 구할 수 있다.
t = 1111, R = 100
t mod R = 0011
(T mod R)N^(-1) mod R 도 마찬가지로 R 이상의 비트를 날리면 된다.
2번을 보면 (T+mN)/R 이 정수 이므로 R이 2의 거듭제곱이면 비트 쉬프트 연산을 통해 t 를 구할 수 있다.
t = (T+mN) >> log2(R)
몽고메리 감산 알고리즘의 return 값인 t는 TR^(-1) mod N 이다.
왜인지는 아래의 증명을 통해 이해하자.
(T + mN)/R 이 정수인 이유
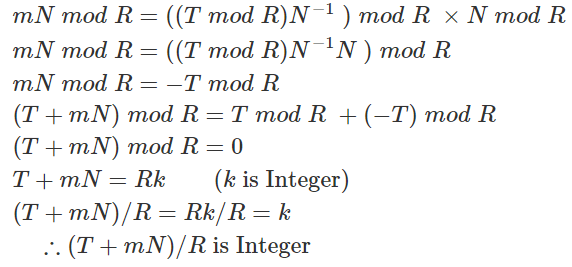
return 값인 t가 TR^(-1) mod N 인 이유
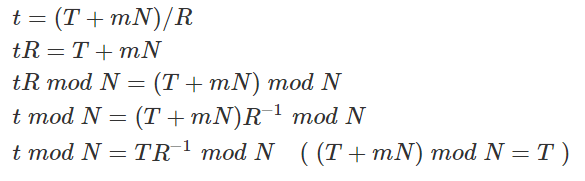
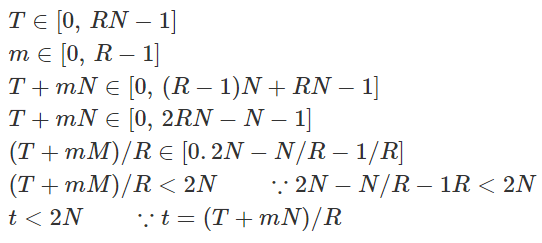
마지막으로 if 부분을 보면
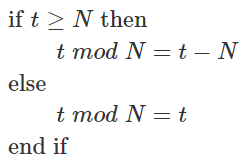
t < 2N 이므로 t가 N보다 크거나 같을 경우 t - N을 빼주면 t mod N 의 결과가 나오며,
t 가 N보다 작을 경우 t의 값 그대로가 t mod N 이다.
따라서 TR^(-1) mod N을 계산하는데 있어서 Montgomery Reduction 알고리즘을 사용하면 나눗셈 연산을 비트연산자를 통해서 계산할 수 있다. (R이 2의 거듭제곱인 경우)
Example
알고리즘의 예시를 들자면
R = 10, N = 17, a = 7, b = 15 이라 하면,
-5R + 3N = -5 * 10 + 3 * 17 = 1이므로 N^(-1) = 7
a의 b의 Montgomery Form 은
aR mod N = 7*10 mod 17 = 2
bR mod N = 15*10 mod N = 14
알고리즘의 입력인 T는 (aR mod N)*( bR mod N ) = 2*14 = 28
T = 2 * 14 = 28 < RN = 170 으로 몽고메리 감산 알고리즘의 조건인 T <= RN-1 성립
T mod R = 8, N^(-1) = 7 이므로
m = (T mod R)N^(-1) mod R = 8*7 mod R = 6
t = (T + mN) / R = (28 + 6*17) / 10 = 130 / 10 = 13
t = abR mod N = 7*15*10 mod 17 = 13 으로
몽고메리 형식 을 만족한다.