Cryptography
[Cryptograhpy] CRT를 이용한 빠른 RSA 복호화
h34hg0
2022. 10. 29. 22:43
CRT(Chinese Remainder Theorem)를 이용하면 RSA복호화를 기존 복호화 방식보다 빠르게 할 수 있다.
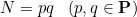
CRT를 이용한 빠른 RSA 복호화 증명
CRT에 의하여


(1), (2)를 만족하는 m이 유일하게 존재.



아래의 식을 위 식의 k에 대입


양변에 q 곱하면
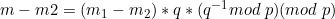
m2 이항

p > q 라고 하면

위 식을 이용하여 복호화 하면
기존 복호화 방법인

보다 빠르게 복호화가 가능하다. (사전에 필요한 값 대부분을 미리 계산하기 때문)
하지만 m1, m2를 아직모르기에 m1 와 m2를 구해보자.
m1, m2 구하기

이므로

이다.
따라서





이고
위수(order)가 페르마 소정리에 의하여 p - 1이므로

이다.
m2도 위와 같은 방법으로 하면 다음과 같다.

이제 m1과 m2를 알았으므로

위 방법을 사용하여 복호화를 할 수 있다.
m1에서 지수를 dp, m2에서의 지수를 dq 라 한다.
PKCS#1
RSA암호 표준 pkcs#1에서는 n = pq일 때, rsa개인키에 대하여 두개의 형식을 나타낸다
1. {n, d}
2. {p, q, dp, dq, qinv}
2의 개인키가 CRT를 이용하기위한 키다.
pkcs#1에 대한 자세한 내용은 RFC 8017문서에 있으니 필요하면 참고
https://www.ietf.org/rfc/rfc8017.txt